Afficionados of puzzles will be acquainted with the Monty Hall Problem, a probability conundrum inspired by the 1960s US game show Let's Make a Deal. In 1975, Steve Selvin sent two letters to the American Statistician essentially presenting the following problem:
Suppose you're on a game show and you're given the choice of three doors. Behind one is a car, behind each of the others is a goat. You pick a door, say door A, and the host, who knows what's behind the other doors, opens another door, say B, which has a goat. He then says: "Do you want to switch to door C?" Is it to your advantage to take the switch?
The two doors available to the contestant, the original choice Door A and the unopened Door C, appear to have an equal probability of having the car. However, this is not so. The table below shows the three possible games that result from the three locations of the car, A, B, and C. We can see that in two out of the three games, there is a car to win if a switch is made. So it is definitely advantageous to make the switch.
| Door A | Door B | Door C | Result | |
| Game 1 | car | goat | goat | lose |
| Game 2 | goat | car | goat | win |
| Game 3 | goat | goat | car | win |
The problem in the form posed above was answered by Marilyn vos Savant in her 1990 "Ask Marilyn" column in Parade magazine. Ms Savant became famous when an entry in the Guinness Book of Records advertised her achievement of obtaining the highest recorded score of 228 on an IQ test. Unfortunately, her analysis of the problem made an unjustified assumption about the strategy employed by the game show host. We can see this by considering that he might do one of the following:
(a) always reveal a goat behind door B or C
(b) randomize his choice between doors B and C
There is nothing in the problem as stated above to prevent case (b). While in case (a), the option that Ms Savant assumed, the chance of being successful with a switch is two thirds, for case (b) it turns out to be one half, in other words, there is neither an advantage nor disadvantage in switching. So in 1999, to eliminate case (b) and clarify the game show host's strategy, Peter Mueser and Donald Granberg of the University of Missouri recast the enigma as follows:
A thoroughly honest game-show host has placed a car behind one of three doors. There is a goat behind each of the other doors. You have no prior knowledge that allows you to distinguish among the doors. "First you point toward a door," he says. "Then I'll open one of the other doors to reveal a goat. After I've shown you the goat, you make your final choice whether to stick with your initial choice of doors, or to switch to the remaining door. You win whatever is behind the door." You begin by pointing to door number 1. The host shows you that door number 3 has a goat. Do the player's odds of getting the car increase by switching to door number 2?
In this version, the game show host explicitly declares his intention to reveal a goat. I often wondered what the contestant did with the poor beast when he won it, after all, no one wants a goat munching their Sunday newspaper while trying to digest the latest financial news.
The Monty Hall Problem is a famous problem and it serves as the inspiration behind this week's poser.
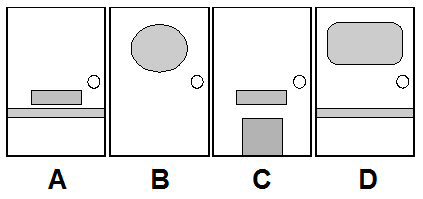
Behind one of four glass doors is concealed a car. Door A has a letterbox and a pushbar, B shows an oval window, C exhibits a letterbox and a catflap, and D has a rectangular window and a pushbar. Which door is to be opened to reveal the car?
Solution next Sunday
Last Week's Puzzle
To solve The Unspotted Die Puzzle, it can be seen that the four dice are constructed from the digits 6593. Each digit gives the total of the number of visible spots on that die. Since the last digit is 3 and one spot is showing then there are two missing.









